Linia algebro por Despero (parto 1)
Ĉi tio estas reskribaĵo de mia propra resumo pri linia algebro por kreado de flatbox ludmotoro. Ĝi estas uzata por mi kiel kaŝoslipeto, sed vi povas uzi ĝin por vi mem (se vi trovos ĝin utila). Dankon al ashen-aetna!
Matricoj
Matrico estas ortangula tabelo kun datenoj nomataj elementoj. Multipliko de matricoj al vektoroj:
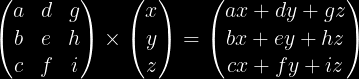
Do ni povas prezenti vektoron V kiel multipliko:
Reguloj de linieco
Se:
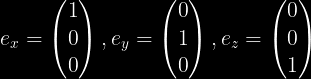
do:
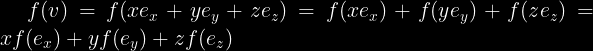
Neliniaj funkcioj
Tiuj estas funkcioj, kiuj ne obeas la regulojn de linieco. Ekzemple:
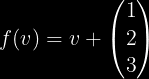
Se V = W, do:
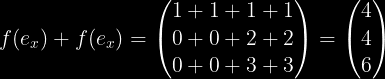
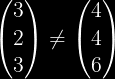
Kvaroblaj vektoroj kaj matricoj
Ĉiu 3x3-matrico povas esti reprezentita kiel 4x4-a:
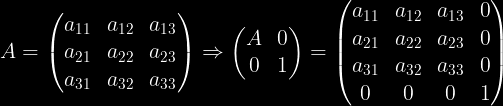
Vektoron V kun aldona kvara komponanto “1” ni povas prezenti kiel multipliko:
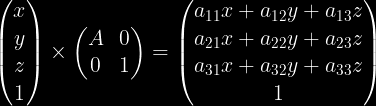
Nun ni transformigos nian “nelinian” funkcion en linian:
do:
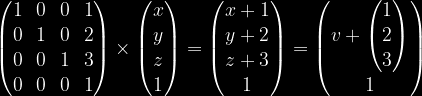
Projekcioj
Linio traiganta iun punkton X kun direkto (vektoro) V estas aro de punktoj, kiuj povas esti atingitaj per aldonado de kelkaj V al X en simboloj:
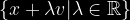aŭ:
Se:
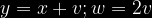
tiam:
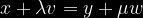
Do:
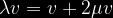
Du linioj estas paralelaj, se ili havas saman direkton:
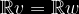
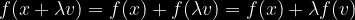
Konvertado de paralelaj linioj per linia mapo:
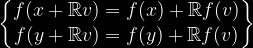
Homogenaj koordinatoj
Homogenaj koordinatoj havas tian econ, ke la objekto, kiun ili difinas, ne ŝanĝiĝas, kiam ĉiuj koordinatoj estas multobligitaj per la sama ne-nula nombro.
(punkto A estas centro de placo X)
Movado de punktoj dekstren po t:
