Linia algebro por Despero (parto 2)

La dua parto de linialgebra resumo por flatbox ludmotoro. Parto 1

Utilaj formuloj

• longeco de vektoro

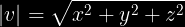
• ununormigo de vektoro

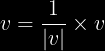
(la direkto estas sama, sed la longeco estas “1”, V != 0)

Anguloj inter vektoroj

Kiel distingi pozitivajn kaj negativajn angulojn?

1. Neniel. En kelkaj kazoj ni vere zorgas pri angulo “inter … kaj …“, sed ne angulo “de … ĝis …“, tiuokaze la signo ne gravas, do ni ne devas difini ĝin.
2. Ni precizigas, ĉirkaŭ kiu akso ni rotacias, kaj difinas, kiu direkto de rotacio respondas al pozitiva rotacio. Ekzemple se rotacio de e_x ĉirkaŭ e_z per +π/2 rezultiĝas al e_y:

Sinuso kaj kosinuso

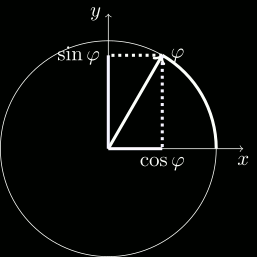
La punkto en la supro de la unuopa vektoro, komencanta de la origino, kiu havas angulon φ al la X-akso, estas:

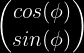
Do:

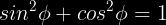
Rotacio en 2D (per matricoj)

Oni diru, ke ni havas rotacion R kun angulo φ ĉirkaŭ Z-akso:

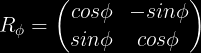
1. Unua kolumno estas rezulto de rotacio de e_x
2. Dua kolumno estas rezulto de rotacio de e_y

Se ni havas kelkajn rotaciojn (ekz. φ₁ kaj φ₂), tiam φ = φ₁ + φ₁:

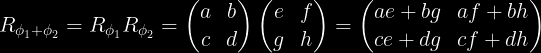
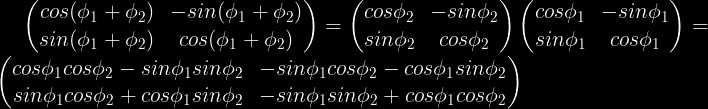
Do ni havas sekvajn identecojn:

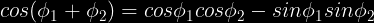
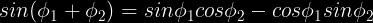
Komputado de angulo inter du vektoroj

1. Ĉar angulo inter rotataj vektoroj ne ŝanĝiĝas, do ni transformas V₁ (kun angulo φ₁) al e_x – intreprena rotacion -φ₁ (do subtraho):

   

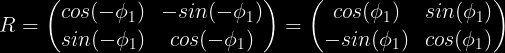
   Pruvado:

   

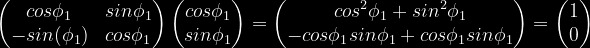
2. Ni komputas angulon inter e_x kaj la turnita V₂:

   

   

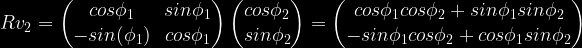
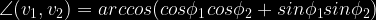
   Do:

   

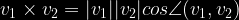
Orteco

Angulo inter du vektoroj estas orta, se ĝia kosinuso estas 0 (tio estas V₁ x V₂ = 0).

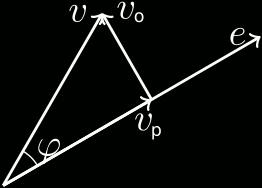
Ni povas malkomponi unu el du vektoroj V kaj E en du partojn: unua (V_p) kun la sama direkto kiel E kaj dua (V_o) ortan al ĝi. Se |V| = 1, tiam |V_p| = cosφ.